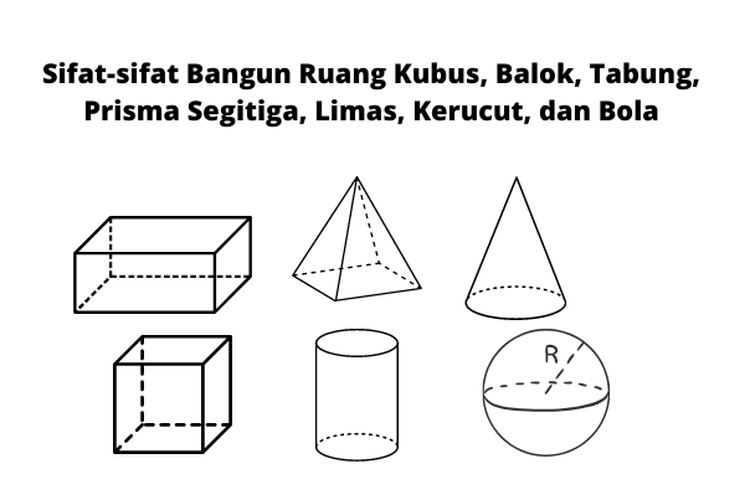
Kubus dan balok adalah dua bentuk bangun ruang yang sering diajarkan dalam pelajaran matematika. Keduanya memiliki kesamaan dan perbedaan yang penting untuk dipahami, terutama bagi siswa SD atau SMP. Ciri-ciri kubus dan balok tidak hanya menjadi dasar dalam memahami geometri, tetapi juga membantu dalam menyelesaikan berbagai masalah terkait luas permukaan, volume, dan sifat-sifat bangun ruang.
Kubus dan balok memiliki struktur yang mirip, yaitu sama-sama memiliki 6 sisi, 12 rusuk, dan 8 titik sudut. Namun, setiap bentuk memiliki karakteristik unik yang membedakannya. Dalam artikel ini, kita akan membahas secara lengkap tentang ciri-ciri kubus dan balok, termasuk pengertian, sifat-sifat, serta perbedaan antara keduanya. Penjelasan ini akan disajikan dengan bahasa yang mudah dipahami dan dilengkapi contoh soal agar lebih praktis.
Selain itu, kita juga akan melihat bagaimana ciri-ciri kubus dan balok dapat diterapkan dalam kehidupan sehari-hari. Contohnya, banyak benda di sekitar kita yang berbentuk kubus atau balok, seperti kotak makanan, buku, atau lemari. Memahami ciri-ciri bangun ruang ini akan memudahkan kita dalam menghitung luas permukaan dan volume, serta memahami struktur tiga dimensi dari suatu objek.
Mari kita mulai dengan penjelasan mengenai apa itu kubus dan balok, serta sifat-sifat utamanya.
Pengertian Kubus dan Balok
Kubus adalah sebuah bangun ruang tiga dimensi yang dibatasi oleh enam bidang datar yang berbentuk persegi. Setiap sisi kubus memiliki ukuran yang sama, sehingga semua rusuknya memiliki panjang yang sama pula. Contoh benda yang berbentuk kubus adalah dadu, kotak permainan, atau rubik.
Sementara itu, balok adalah bangun ruang tiga dimensi yang dibatasi oleh enam bidang datar yang berbentuk persegi panjang atau persegi. Balok memiliki tiga pasang sisi yang berhadapan dan sama besar, namun ukurannya bisa berbeda-beda. Contoh benda yang berbentuk balok adalah kotak makanan, lemari, atau buku tebal.
Baik kubus maupun balok merupakan bagian dari bangun ruang yang termasuk dalam materi geometri. Mereka memiliki ciri-ciri tertentu yang membuatnya mudah dikenali dan dibedakan satu sama lain.
Ciri-Ciri Umum Kubus dan Balok
Kedua bangun ruang ini memiliki beberapa ciri-ciri yang sama, meskipun ada juga yang berbeda. Berikut adalah ciri-ciri umum yang dimiliki oleh kubus dan balok:
-
Memiliki 6 sisi
Baik kubus maupun balok memiliki 6 sisi. Sisi-sisi tersebut terdiri dari tiga pasang sisi yang saling berhadapan. Pada kubus, semua sisi berbentuk persegi, sedangkan pada balok, sisi-sisi bisa berbentuk persegi atau persegi panjang. -
Memiliki 12 rusuk
Rusuk adalah garis yang menghubungkan dua titik sudut. Baik kubus maupun balok memiliki 12 rusuk. Pada kubus, semua rusuk memiliki panjang yang sama, sedangkan pada balok, rusuk-rusuk memiliki panjang yang berbeda-beda. -
Memiliki 8 titik sudut
Titik sudut adalah pertemuan tiga rusuk. Kedua bangun ruang ini memiliki 8 titik sudut, yang merupakan bagian penting dalam menentukan bentuk dan struktur bangun ruang. -
Memiliki diagonal bidang
Diagonal bidang adalah garis yang menghubungkan dua titik sudut yang berada pada sisi yang sama. Kedua bangun ruang ini memiliki 12 diagonal bidang. -
Memiliki diagonal ruang
Diagonal ruang adalah garis yang menghubungkan dua titik sudut yang tidak berada pada sisi yang sama. Kubus dan balok masing-masing memiliki 4 diagonal ruang. -
Memiliki bidang diagonal
Bidang diagonal adalah bidang yang dibentuk oleh dua diagonal bidang dan dua rusuk. Kubus dan balok memiliki 6 bidang diagonal. -
Memiliki luas permukaan dan volume
Keduanya memiliki rumus untuk menghitung luas permukaan dan volume. Luas permukaan mengukur total area permukaan bangun ruang, sedangkan volume mengukur ruang yang dapat diisi oleh bangun tersebut.
Perbedaan Antara Kubus dan Balok
Meskipun kubus dan balok memiliki ciri-ciri yang sama, terdapat beberapa perbedaan mendasar antara keduanya. Berikut adalah perbedaan utama antara kubus dan balok:
- Bentuk Sisi
- Kubus: Semua sisi berbentuk persegi.
-
Balok: Sisi-sisi bisa berbentuk persegi atau persegi panjang.
-
Panjang Rusuk
- Kubus: Semua rusuk memiliki panjang yang sama.
-
Balok: Rusuk-rusuk memiliki panjang yang berbeda-beda (panjang, lebar, dan tinggi).
-
Bentuk Dasar
- Kubus: Bentuk dasar adalah persegi.
-
Balok: Bentuk dasar adalah persegi panjang.
-
Rumus Volume dan Luas Permukaan
- Kubus:
- Volume = $ s^3 $ (s = panjang sisi)
- Luas permukaan = $ 6s^2 $
-
Balok:
- Volume = $ p \times l \times t $ (p = panjang, l = lebar, t = tinggi)
- Luas permukaan = $ 2(pl + lt + pt) $
-
Simetri
- Kubus memiliki simetri yang lebih sempurna karena semua sisi dan rusuknya sama.
- Balok memiliki simetri yang lebih terbatas karena ukuran sisi dan rusuk berbeda.
Contoh Soal dan Pembahasan
Untuk memperdalam pemahaman, berikut adalah contoh soal beserta pembahasan mengenai kubus dan balok:
Contoh 1:
Sebuah kubus memiliki panjang sisi 5 cm. Hitunglah luas permukaan dan volume kubus tersebut!
Jawab:
– Luas permukaan = $ 6s^2 = 6 \times 5^2 = 6 \times 25 = 150 $ cm²
– Volume = $ s^3 = 5^3 = 125 $ cm³
Contoh 2:
Sebuah balok memiliki panjang 10 cm, lebar 6 cm, dan tinggi 4 cm. Hitunglah luas permukaan dan volume balok tersebut!
Jawab:
– Luas permukaan = $ 2(pl + lt + pt) = 2(10×6 + 6×4 + 10×4) = 2(60 + 24 + 40) = 2×124 = 248 $ cm²
– Volume = $ p \times l \times t = 10×6×4 = 240 $ cm³
Kesimpulan
Kubus dan balok adalah dua bentuk bangun ruang yang memiliki ciri-ciri yang serupa, tetapi juga memiliki perbedaan yang jelas. Dengan memahami ciri-ciri kubus dan balok, kita dapat lebih mudah mengidentifikasi bentuk-bentuk bangun ruang, serta menghitung luas permukaan dan volume dengan tepat.
Pemahaman tentang kubus dan balok juga sangat berguna dalam kehidupan sehari-hari, terutama dalam bidang konstruksi, desain, dan ilmu teknik. Selain itu, belajar tentang bangun ruang ini juga memberikan dasar yang kuat untuk mempelajari bangun-bangun ruang yang lebih kompleks, seperti prisma, limas, dan tabung.
Dengan demikian, memahami ciri-ciri kubus dan balok adalah langkah penting dalam memperluas wawasan matematika dan meningkatkan kemampuan analitis dalam menyelesaikan berbagai masalah geometri.